Statistical Forecasting in Kanban

The inherent flexibility and pull-based approach of the Kanban method make it perfectly suitable for high-variability environments. At the same time, high variability is what makes planning and delivery predictions challenging. Deterministic forecasting - one based on fixed dates and deadlines - is likely to fail in those contexts, as it tends to ignore throughput and cycle time fluctuations. Statistical or probabilistic forecasting, therefore, serves as a critical enabler of realistic, reliable workflow planning.
To probabilistically forecast work delivery, a team needs to leverage past performance data - throughput and cycle time - also taking into consideration variable work item characteristics. With that, it’s possible to outline predictive distributions, not just single-point estimates.
When managing work with Kanban, each task has a cycle time record: the time elapsed between initiation and completion. The accumulation of past cycle times forms a robust, trustworthy distribution, describing the system’s behavior under specific conditions. Sampling these distributions enables teams to make probabilistic estimates for their future work delivery rates.
Monte Carlo simulation is a crucial aid to this process. It involves repeatedly drawing from historical cycle-time dispersion to simulate multiple possible completion scenarios for a given set of work items. The result is a range of outcomes with respective confidence levels, for example, a 90% chance that a set of 20 features will be done within 12 to 18 days. Unlike deterministic estimates, this approach expresses both expected delivery and unavoidable uncertainty.
Cycle time distributions
Probabilistic forecasting is impossible without accurate measurements and a solid grasp of cycle time distributions. In a Kanban-based workflow, cycle times tend not to follow a normal distribution - because of task complexities and a varying team load, it’s more common for the distribution to be skewed, multi-modal, or heavy-tailed. Replacing these characteristics with simplistic averages can lead to overconfidence and planning errors. Probabilistic projections embrace the real-life distributions, retaining nuances such as intermittent delays or periods of increased throughput.
Illustrating these distributions with histograms, cumulative flow diagrams, and cycle-time scatter-plots allows teams to find patterns and anomalies. For example, continuous long-tail cycle times may suggest systemic bottlenecks or team constraints, informing both the planning estimates and process improvement efforts.
Historical Cycle Time Distribution Example
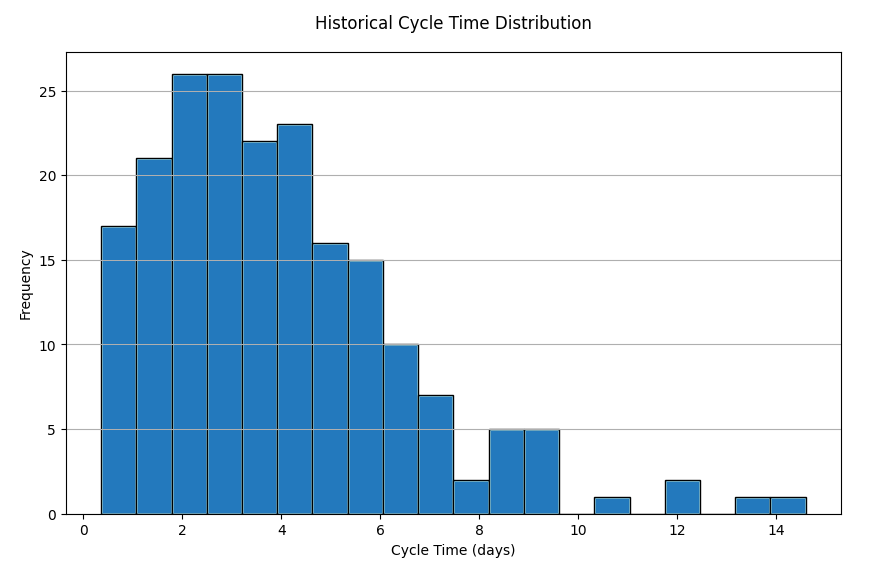 A skewed distribution, with most items completing in ~2–6 days, and a long tail extending to ~10 days; reflective of real Kanban variability, and the importance of modeling distributions rather than averages.
A skewed distribution, with most items completing in ~2–6 days, and a long tail extending to ~10 days; reflective of real Kanban variability, and the importance of modeling distributions rather than averages.
Throughput in forecasting
Where cycle time measures individual task completion speed, throughput captures system capacity over time. Reviewing the work items count a team completes per week or month also feeds probabilistic estimation. A combination of cycle time and throughput measurements creates mutually complementary perspectives: the cycle time predicts the time needed for tasks or task batches, while throughput signals the rate at which the system can sustain delivery.
For many teams, throughput variability is often harder to understand than cycle time fluctuations. A team may sustain stable averages, but variations resulting from holidays or staffing changes - not to mention task complexity - tend to cause wide delivery ranges. To forecast probabilistically, such fluctuations mustn’t be ignored, but quantified.
Cumulative Probability Curve Example
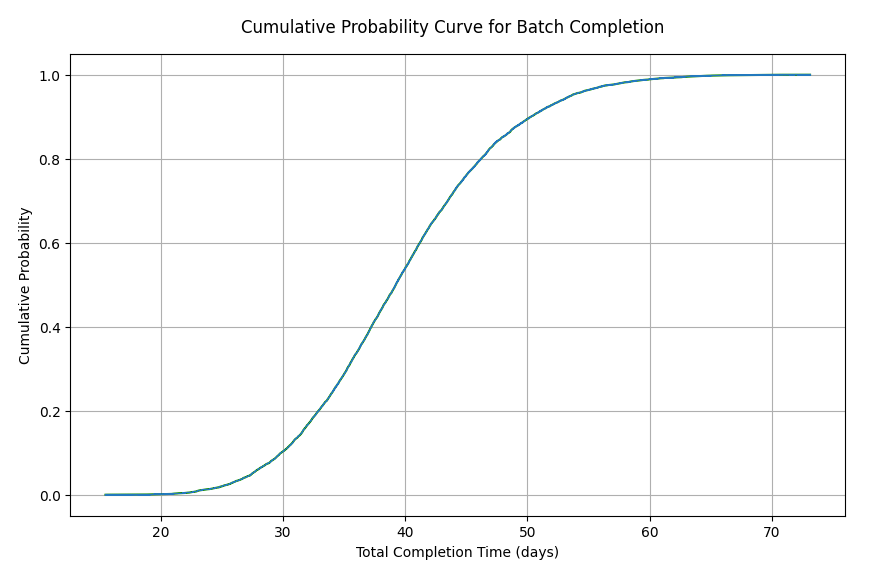
- 50% of batches complete within ~39 days
- 70% of batches complete within ~43 days
- 90% of batches complete within ~50 days
How to apply a Monte Carlo simulation?

Monte Carlo simulation computationally analyzes synthetic project outcomes. For cycle time distributions, the process can be broken down into:
Step 1: Prepare inputs
Gather historical cycle time data for a sufficient sample size; validate it for consistency, and remove outliers if necessary.
Step 2: Sample randomly
For every simulated iteration, randomly sample cycle times for each work item based on historical distributions.
Step 3: Aggregate
Sum individual cycle times to outline the completion time for a batch or project.
Step 4: Iterate
Run the simulation thousands of times to generate a probability distribution of potential completion dates.
Step 5: Analyze
Calculate confidence intervals (e.g., a 70% chance the work will be completed by a selected date), forecast expected completion times (most commonly, the mean or median of the completion date distribution), and set probabilities of hitting specific delivery targets.
The outcome is a full probability distribution of possible delivery dates, not a single forecast. It shows how probable potential completion dates are, which makes uncertainty explicit and allows managers to make commitments aligned with their risk tolerance. For instance, a 70% confidence interval may be suitable for internal planning, but a 90% confidence interval would be likely to guide external stakeholder expectations.
Monte Carlo Simulation Example
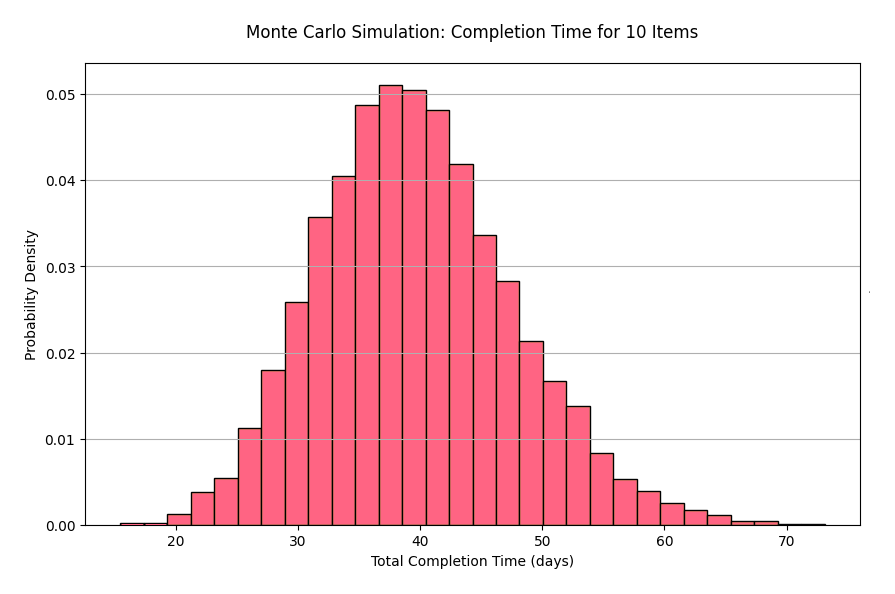 Simulated total completion times for 10 items from 10,000 iterations; peak probability density sits around 35 and 40 days, with lower probability for extreme totals - illustrating uncertainty in batch delivery.
Simulated total completion times for 10 items from 10,000 iterations; peak probability density sits around 35 and 40 days, with lower probability for extreme totals - illustrating uncertainty in batch delivery.
Integrating statistical forecasting into Kanban
Probabilistic forecasting seamlessly aligns with Kanban’s underlying Lean principles - an emphasis on flow optimization and variability management. Intentional accounting for uncertainty means avoiding false precision and minimizing pressure to conform to arbitrary deadlines. Decisions are based on observed system behavior, not top-down dictated assumptions.
Practical integration considerations:
Data gathering discipline: The accuracy of cycle time tracking is essential, so teams must use consistent definitions of start and end points for tasks, including subtasks and hand-offs.
Visualization aids: Team Kanban boards could be equipped with probabilistic forecasting displays, drawn from historical performance. Having access to cumulative flow diagrams, cycle time scatter-plots, or Monte Carlo forecast curves delivers actionable insights at each step of the process.
Did you know?
You don’t have to measure cycle time, throughput, or CFDs manually - the Kanban Tool® platform automatically generates key metrics directly from your board. With built-in cumulative flow diagrams and cycle-time tracking, probabilistic forecasting becomes practical and easy to apply. Give your projects reliable delivery forecasts today!
Scenario planning: For mature implementations, the forecasts could also inform what-if analysis; for instance, what happens when the WIP limit increases, or an urgent item enters the system. Probabilistic simulations enable speedy evaluation of possible choices.

Benefits & limitations
The direct value of using probabilistic forecasting lies in realistic delivery estimates, but the benefits also impact broader organizational learning. Through quantifying uncertainty, teams can easily identify high-risk commitments and manage them proactively. Stakeholders become aware of the existing variability and should be less prone to perceiving deviations from estimates as a failure. Analyzing cycle time distributions over time often highlights inefficiencies and bottlenecks, driving ongoing refinement of the workflow. Lastly, marrying throughput forecasting with work intake policies allows teams to plan sustainable workloads, avoiding over-commitment and crunch.
Because the method relies on historical information quality and relevance, rapid shifts in team composition, used technology, or project scope can invalidate prior delivery distribution estimates. Furthermore, interpretation of probabilistic outputs assumes statistical literacy; stakeholders could misread a 70% confidence interval as a guarantee rather than a likelihood.
The future of probabilistic forecasting
Advances in data analytics, and AI in particular, are bound to enhance probabilistic forecasting capabilities. Machine learning algorithms can model complex dependencies between tasks and detect patterns in cycle times, allowing for dynamic prediction adjustments. When coupled with real-time Kanban boards and automatically generated workflow analytics, these techniques certainly promise a future with increasingly accurate and low-maintenance forecasting.